Planning of Water and Hydropower Intake Structures (GTZ, 1989, 122 p.) 5. Sand trap 5.1 Necessity for sand traps 5.2 Hydraulic design

Planning of Water and Hydropower Intake Structures (GTZ, 1989, 122 p.)

5. Sand trap

5.1 Necessity for sand traps

Sand traps are necessary when the suspended matter content of the river water is high and when plant components such as pressure pipes, turbine rotors, slide valves, etc., must be protected from abrasion by hard suspended matter such as quartz sand.

Wear and tear due to abrasion can in a short time result in serious damage and in the case of turbines in a considerable reduction in efficiency. The greater the effective head and, thus, the flow velocity, the greater the danger to the plant components.

It is the purpose of the sand trap to remove the fine-grained suspended matter from the water and to protect the components. This is achieved most simply by allowing the suspended matter to settle in the settling basin or a long sand trap. This is done by slowing down to a low velocity the amounts of water distributed as evenly as possible over the cross-section of the basin. The time of passage through the basin must not be shorter than the settling time of the suspended matter. These boundary conditions require long structures suitably shaped from the hydraulic point of view (cf. section 5.3).

The velocity of the water in the inlet canal of the sand trap must not be low, otherwise suspended matter will be deposited in the inlet canal too soon. The flow into the basin is therefore turbulent. A well-designed transition section should be arranged ensuring a steady and even passage; likewise, stilling screens can be used here and achieve good results (cf. Fig. 44).

5.2 Hydraulic design

As the plant components coming into contact with the water such as slide valves, pressure pipes, turbines, rotors and casings are destroyed by the suspended matter, it is necessary to determine its concentration and composition.

Fig. 44: Schematic representation of a uniformly loaded sand trap

In general, the suspended matter is found to be composed of particles of different sizes. In rivers in the lowland or in the low mountain ranges, the colloidal particles can be of diameters from the mud fraction to the sand fraction (f 0.002 mm to 0.2 mm or ~1 mm), whereas in mountain rivers with steep slopes, the particle sizes can be of the order of 2 to 3 mm.
The quantity of suspended matter is expressed by the suspended matter concentration:

suspended matter concentration =

kg suspended matter / m³ water

Suspended matter concentrations (C) are generally

- in lowland rivers C = 0.1 to 1.0 kg/m³,
- in mountain rivers/brooks C = 2.0 to 10 kg/m³ .

According to the nature of the catchment areas (topography, geology, utilization, vegetation), these values can be far exceeded or not reached. Thus the suspended matter concentration in the lower course of the Yellow River in China varies seasonally between 60 and 600 kg/m³ [9].

The suspended matter concentration can be measured by sampling (cf. section 1.3.3) and assessed by inspection (clear water through which the bottom is visible has a low suspended matter concentration whereas turbid, yellowish brown water indicates a high suspended matter concentration).

The suspended matter content varies from season to season and depends upon the precipitation in the catchment area and the regime of the river or stream.

5.2.2 Desanding measure

The desanding measure is expressed by the ratio of the suspended matter concentration of the desanded water for power generation Cperm. to the suspended matter concentration C of the river water which has not been desanded:

degree of desanding = 100 C_perm./C (in %).

There are no regulations or standards for the selection of the degree of desanding; empirical values which have been derived from the operation of existing hydroelectric power plants are rather taken as a basis.

Decisive criteria for fixing the degree of desanding are:

- minimization of the damage caused by suspended matter (abrasion, etc.) to the plant components.
- sensitivity of the turbines to suspended matter depending upon the turbine type, the diameter of the suspended matter particles, the mineralogical nature of the particles, the effective head.

Experience has shown that

- cross-flow turbines are relatively insensitive to soft impurities such as silts, clays and floating matter such as grass, leaves, etc.
- Kaplan turbines, Francis turbines and Pelton turbines are more sensitive to any kind of suspended matter, the Pelton turbine used in micro. and mini-plants being less severely affected by impurities in the water. It is possible, however, that wear and tear on the buckets sharply increases.

The permissible suspended matter concentration is also determined by the definition of the grain-size limit of the particle which is only just to be separated by the sand trap.

5.2.3 Determination of the grain-size limit

With regard to the above-mentioned criteria and the requirements of operation, the indication of the particle diameter serves to define a limiting size of the suspended matter which is only just allowed to deposit. From experience it may be assumed that:

(a) for low-head power plants:
d_limit. = 0.2 to 0.5 mm
(b) for medium and high-head power plants:
d_limit. < 0.1 to 0.2 mm
(c) for 100 m head and more:
d_limit. £ 0.01 - 0.05 mm.

If the particles to be deposited consist of quartz sands, the lower limiting values apply. The values given under (c) can also be fixed for economic reasons when the particle fractions consist of particularly hard minerals (quartz, feldspar, garnet, etc.).
According to Keller [10], small hydroelectric power plants can be referred to as high-head power plants according to the following rule of thumb:

where Q = design discharge in m³/s, h = total head in m.

The pipelines for the water for power generation of such plants are usually very long (at relatively small discharge cross-sections), i.e. they are pipelines under high internal pressure.

Low-head power plants have heads h £ 10 m.

All plants between high-head and low-head power plants are therefore medium-head power plants.

If the above-mentioned grain-size limits are considered for different types of plant and if it is assumed that small hydroelectric power plants usually have heads £ 100 m, it can be concluded that the limiting particle diameter to be separated

- can in the normal case be fixed at 0.2 mm,
- should only in exceptional cases be selected with d_limit. = 0.05 mm.

(Exceptions:

- head ³ 100 m,
- mineral: pure quartz or similar,
- turbine type: Francis/cross-flow turbine).

Owing to an extension of the cross-section, the water flowing into the sand trap is so slowed down that the suspended matter particles can no longer be maintained in suspension and sink (cf. section 5.1).

The water particles entering and the suspended matter particles transported by them horizontally at an even velocity must reach the end of the basin only when the sinking process is completed, i.e. the sinking time ts must be shorter than the time of passage (translation time) td through- the basin (Fig. 45).

Fig. 45: Longitudinal section of sand trap. Schematic path curve of a settling sand particle "K" under the influence of turbulence. v_d flow velocity in the basin, v_s sinking velocity in stagnant water, w dynamic buoyancy due to turbulent flow; condition: t_d ³ t_s

The actual sinking velocity of the particles is then

v_S' = v_S - w (in m/s)

where w is essentially a function of the mean flow velocity in the basin. With the estimated value

w= a v_d with a = 0.04 [11].

v_s' = v_s - 0.04 v_d (in m/s).

For the settling process (Fig. 45) the following relationships result:

1 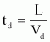(in s),

with L = effective basin length in m, v_d = mean flow velocity in m/s, and

2 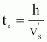(in s),

with h = effective sand trap depth in m, v_s' = mean sinking velocity.
A rectangular cross-section of the sand trap results in the following relationship:

3 v_d = Q/(B h) (in m/s),

with Q = discharge in m³/s, B = basin width in m, h = sand trap depth in m. By transformation and using the limiting relationship t_d = t_s, we have

4 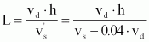(in m).

As can be seen, the denominator can assume a negative value. If this is the case, settling is not possible under the conditions assumed. It follows that the determination of the sinking velocity vs is of the utmost importance. According to Popel [12], vs is a function of the water movement, the state of flow in the water, the kinematic viscosity, the shape and size of the suspended matter, and of the specific weight of the particles.

The sinking velocity heavily depends upon the state of flow around the particle during sinking, and therefore also on the Reynolds' number.
The following is valid:

R_e < 1 Stokes' law (laminar flow)

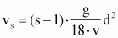
with d = particle diameter, s = density of particles due to density of water (2.6 to 2.7 for sand), n = kinematic viscosity of water (0.0132 cm²/s at 10°C in clean water), g = acceleration due to gravity = 9.81 cm/s².

Re > 2000 Newton's law

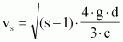
with c = coefficient of resistance of the particles (0.5 for round particles).

1 < R_e < 2000

range of transition according to Rubey.

Fig. 1 in Annex 11 shows the sinkingvelocity vs according to the relationships above. In the sand trap itself the flow is turbulent, with a Reynolds' number of

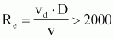
with D = equivalent diameter (4 F/U = 4 (B h)/(B + 2h)), B = basin width, h = sand trap height (effective), F = cross-sectional area (cross-section of sand trap), U = wetted perimeter.
Therefore the sinking velocity v_s (according to Fig. 1 in Annex 11) must be reduced accordingly and introduced into formula 4. The flow velocity v_d must not exceed an upper value in order

- to allow the suspended matter to sink,
- to prevent suspended matter which has already settled being washed away,
- to prevent sinking suspended matter being brought into suspension again.

This velocity, which is to be considered the limiting value, can be treated as being equivalent to the "critical velocity" known from the bed load theories. According to Camp [13], this critical velocity is

(in cm/s)

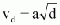
with d = particle diameter, a = coefficient as a function of d, a = 36 at d > 1 mm, a=44 at 1 mm > d > 0.1 mm, a = 51 at d < 0.1 mm.

For d = 0.2 the following results:

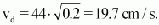
In practice, a mean flow velocity of

v_d = 0.2 m/s

has proved effective.

By transformation of 1

v_d = L / t_d

and introduction into 3, the following relationship is obtained:

5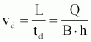

® Q_td= L x B x h

i.e. the volume of the sand trap must be equal to the amount of water flowing in in the unit of time of the residence time (time of passage or sinking).

When the flow velocity vd is known, the dimensions of the basin can be determined. As the length and width construction elements of the sand trap are less costintensive than the depth (foundation, soil excavation, etc.), the depth h is selected.

For small hydroelectric power plants, h should be between 0.5 and 2 m.

When h, v_s and v_d have been inserted in 4, L can be determined.

With V_d, h and Q, B can be determined from 5.