Planning of Water and Hydropower Intake Structures (GTZ, 1989, 122 p.) 3. Hydraulic operation and calculations 3.1 General 3.2 Hydraulic calculation of the free overfall weir 3.3 Free overfall side weir 3.4 Outflow below a dam wall (sluice) 3.5 Intake with a repelling groin 3.6 Hydraulics of the bottom intake (Tyrolean intake)

Planning of Water and Hydropower Intake Structures (GTZ, 1989, 122 p.)

3. Hydraulic operation and calculations

3.1 General

In the following, simple methods of calculation are given for the most important structures. The annexes contain numerical examples which make mathematical procedures simple to understand.

The mathematical procedures for the individual components of an intake structure are in many cases the same. Thus the course of calculation and the formulas to be applied are the same for the retaining weir in the river and the free overfall weir in the lateral intake, e.g. between forebay and diversion canal (Fig. 26).

The most important calculations necessary for the design of the intake structure relate to

- free overfall weir as a retaining or diversion weir,
- discharge below a dam wall in the canal,
- free overfall side weir as spillway or as structure for intake on the river bank,
- bottom intake in a special case,
- lateral intake with repelling groin.

Irrespective of whether intake structures are selected with or without damming of the river, the structures should be so designed that

- at times of the lowest discharge, the required amount of water Q_A can always be diverted,
- all floods, including the design flood, can be evacuated without damage being caused to structures or objects, or danger to life and limb,
- the amount of water flowing into the canal is limited to the amount of water to be diverted QA This can be achieved by installing suitable structures in the inlet or by spillways.

Fig. 32: Limitation resp. evacuation of diverted water through a weir or a sluice

3.2 Hydraulic calculation of the free overfall weir

For calculation purposes, the intake structure or weir is assumed to be as schematically represented in Fig. 33. If the weir is constructed at right angles to the river or the intake so that the water's approach is vertical, the discharge over the weir can be determined by means of the following formula:

Fig. 33: Dimensioning of fixed weirs

Weir formula (or Poleny formula)

(in m³/s)

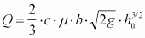
The symbols are as follows (cf. Fig. 33):

Q = discharge over the downstream face in m³/s, c = correction factor for submerged overfall, m = weir coefficient, b = weir crest width in m, g = acceleration due to gravity = 9.81 m/s², h_ü = weir head in m.

- Weir coefficient m

This coefficient depends upon the crest form of the weir. In Fig. 33 the coefficients are given for the most typical crest forms. For the construction of weir bodies with vertical headwater side in rivers transporting a large amount of bed load, it should be remembered that after a prolonged period of operation, this weir will have the same effect as a broad, round-crested weir due to the alluvial deposits in front of the weir face. In this case, the discharge capacity would be smaller due to the smaller weir coefficient.

- Correction factor c

The correction factor c allows for the influence of the tail water level upon the discharge over the weir:

- for the free overfall c = 1,
- for the submerged overfall, c is to be taken from the graphical representation in Fig. 33.

Whether an overfall is free or submerged depends upon the height of the tail water level in relation to the position of the weir crest (Fig. 34).

- If h' < 0, the overfall is free.
- If h' > 0 and if there is a limiting depth t_limit above the weir crest, the overfall is submerged.
- If h' > 0 but the discharge flows over the weir crest, the overfall is submerged.

For the design of a weir, in most cases the height of the weir crest at a given weir length (e.g. width of the river/canal) must be found. For this purpose, the following quantities and dimensions in accordance with the weir type (retaining weir or diversion weir) must be specified or known:

Retaining weir

- maximum discharge (flood event) over the weir
- maximum permissible headwater level h₀
- weir type with weir coefficient tail water level hu when the maximum discharge is evacuated

Fig. 34: Discharge over a weir

Diversion weir

- minimum amount of water to be diverted
- minimum headwater level h₀
- weir type with weir coefficient
- tail water level h_ü when the minimum amount of water to be diverted is evacuated

If these data are available, the weir head h_ü of the retaining weir in the case of flood (maximum load) can be determined. The weir body height is then

w = h₀ - h_ü

This allows the elevations of the water surface in the river upstream of the weir to be determined by the weir formula for any discharge. The weir crest of the intake structure must be high enough so that at the lowest discharge, the required amount of water for power generation is evacuated over the diversion weir by a sufficient weir head (cf. Fig. 35).

Numerical examples of the calculation of a free and submerged overfall weir as well as an overfall over a weir with stilling basin or race floor are given in Annexes 3 to 5.

Fig. 35: Relationship between diversion weir and retaining weir

Fig. 36: Principle of the side weir with the hydraulic characteristics. Q₀ headwater discharge, Q_u tail water discharge, Q_A evacuated amount of water, w weir height, L weir length, h₀ weir head in the headwater, h_u weir head in the tail water, h_m mean weir head, h_Eu energy head in the tail water, v_0,u flow velocity in the headwater, tail water

3.3 Free overfall side weir

A side weir (cf. Fig. 36) is always involved when a weir is approached obliquely or is situated parallel to the channel line to evacuate the amounts of water QA. This oblique approach occurs when the weir is constructed parallel to the river bank or power canal, for example. The calculation of the discharge capacity of a side weir is made with the following weir formula:

(in m³/s)

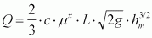
where L = length of side weir in m, h_m = mean weir head in m, m^x = reduced weir coefficient = 0.95 · m (for m cf. Fig. 33), c = correction factor (cf. also section 3.2).

An important prerequisite for the application of this formula is that the discharge in the headwater be a flowing one. This condition is fulfilled when Froude's number is smaller than 0.75:

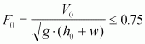
where v₀ = velocity in the headwater in m/s,

(in m/s, for the symbols cf. Fig. 36),

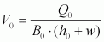
g = acceleration due to gravity = 9.81 m/s²,
h₀ = estimated weir head at the beginning of the side weir in m (cf. calculation example in Annex 6), w = weir crest height in m.
In the place of the weir head h, a mean weir head h_m in m is used. It is the mean value of the smaller weir head ho at the beginning of the side weir which increases along the downstream face up to the maximum weir head h_u at the end of the side weir. The weir head h_u is determined by the discharge characteristic of the river or canal, i.e. it corresponds approximately to the difference between the given tail water level t_u and the weir crest height w.

h_u = t_u - w (in m)

The weir head ho must first be estimated. For this purpose, the known or determined quantities such as weir crest height w, tail water level t_u, inflow to the headwater Q₀, and headwater width B₀ are introduced into the formula

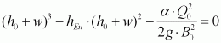
with the energy head

(in m/s, cf. Fig. 36)

(in m/s)

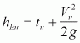
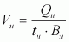
a = 1.1 velocity coefficient

and solved iteratively. After the weir head ho has been determined, the mean weir head

(in m)

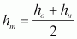
is calculated and the value n read off from the diagram in Fig. 37 as a function of h_m and Q_u > 0 (residual amount of water in the tail water) and/or Q_u = 0 (case: confined tail water; this is the case when the main flow is confined by a sluice and all the water is led over the side weir: Q_A = Q₀). This value n is multiplied by a and yields the new value

a = n a (a= 1.1)

In the above-mentioned formula, this new value a replaces the former value a = 1.1 (n results from Fig. 37).

Repeating the iterative solution of this equation using a we obtain an improved estimated value of h₀.
With the mean weir head then determined, the weir length is

(in m)

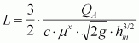
The procedure is shown systematically in the following. A numerical example is given in Annex 6.

Fig. 37: Correction factor n for side weir calculation

3.4 Outflow below a dam wall (sluice)

The calculation of the outflow below a dam wall or a sluice is one of the most common tasks of hydraulic engineering. As compared with the relatively small openings for bottom outlets of dams, the width of the outflow opening for the outflow below the sluice can be considered large compared with its height. In these cases, the discharge can be ,dealt with as a two-dimensional flow problem and calculated with the following formula:

(in m³/s)

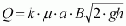
where k = correction factor for submerged discharge; for free discharge k = 1 (cf. Fig. 38), m = discharge coefficient; this coefficient chiefly takes the jet contraction into account, a = height of the outflow opening in m, B = width of the outflow opening in m, h = impounding head in front of the sluice or the dam wall in m, g= acceleration due to gravity = 9.81 m/s².

The discharge coefficient for the vertical sluices which are most frequently used depends upon h/a

m = 0.55 - 0.60 (limiting value)

For rough dimensioning, a value m = 0.6 can be assumed.

The correction factors k for the submerged discharge are given in Fig. 38. For free discharge, i.e. when the tail water is not an influencing factor k = 1.
The tail water is an influencing factor when the shooting jet is impounded at the sluice opening directly behind the sluice (cf. Fig. 38). This discharge behaviour is dependent upon the tail water level (and, thus, upon the dimensioning quantities of the power canal, the headwater level and the sluice opening).

For the dimensioning of the outflow below a sluice, mainly the following quantities are specified or must be fixed:

- height of the sluice opening a (is fixed),
- headwater level (minimum, maximum), known from the canal calculation,
- tail water level h_u (dependent upon the amount of water to be evacuated and upon the dimensioning of the tail water canal),
- sluice width B, dependent upon the canal width.

With the formula given above, Q_A can now be determined. It must first be ascertained whether or not the discharge is free.
For this purpose the ratio h/a is formed.
From Fig. 38d), with, for example, s = 0.7 for h/a, the limiting value h_u/a limit. is determined.

The discharge is free when

Q_A is then determined for the conditions assumed. In most cases, however, the necessary amount of outflow Q_A is known, and therefore only the height of the sluice opening a must be determined.
After these quantities have been fixed, the sluice openings a necessary for the evacuation of the corresponding amounts of water can be determined.
For this purpose, the above-mentioned formula must be transformed with respect toe:

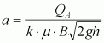
The following procedure is followed:

- If there is a free discharge (i.e. k = 1), the formula given above is used to determine a.
- h/a is formed and the limiting value for h_u/a is ascertained in accordance with Fig. 38d).
- Exist. h_u/a is compared with h_u/a limit. If h_u/a < h_u/a limit., the assumption is correct. The calculation is complete. If the assumption is not correct, the calculation is continued.
- For h_u/a > h_u/a limit., the k value for exist. h_u/a is determined with the curve for h/a from Fig. 38e).
- With this k value Q_Aexist. is calculated; it proves to be smaller than Q_A determined
- In order to evacuate Q_Adeterm. a must be increased. In first approximation, a_new = a/k.
- Now h/a and h_u/a are again checked in accordance with Figs. 38d) and e).
- The k values and the values anew and aold are compared.
- The calculation is repeated by a new adaptation, if necessary, until the deviation is small and QA can be evacuated.

Numerical examples are given for both cases in Annex 7.

Fig. 38: Dimensioning of the discharge below a sluice, d contraction coefficient

a) Discharge below a sluice
b. Free discharge
c) submerged discharge
d) Limit between free and submerged value
e) k value for the submerged discharge as a function of h/a and h_u/a, for d=0.7 as average value, as the influence of d upon k is relatively small.

3.5 Intake with a repelling groin

For this arrangement of the lateral intake, an exact hydraulic determination of the evacuated amounts of water for power generation is not possible, as the inflow into the side canal (power canal) with the aid of a repelling groin very much depends upon the flow conditions and thus also upon the water level in the river.

The rating curves of the river and the canal (relation between water level and corresponding amount of discharge in a river/canal) allow only the approximate amounts of water for power generation to be estimated (cf. Fig. 39).
The amounts of water for power generation are obtained from the water level of the river and of the canal which is identical in the inlet area, thus allowing a value to be estimated for the corresponding discharge.

3.6 Hydraulics of the bottom intake (Tyrolean intake)

In the case of a vertical approach to a Tyrolean intake (cf. Fig. 40), amounts of water partially obstructed by the trash rack - fall into a collection canal which is intended to evacuate the water laterally. With this, a water level similar to that shown in Fig. 40 is formed above the trash rack.

Fig. 39: Lateral intake with repelling groin

The following weir formula is used for the design of a Tyrolean intake:

(in m³/s)

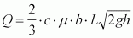
where (cf. also Fig. 40) Q = discharge to be diverted in m³/s, h = k · h_limit. = 2/3 k h_E = "initial water height'' in m, c = 0.6 b cos^3/2 b

with a = inside width between trash rack bars in m, d = centre distance of the trash rack bars in m, b = angle of inclination of the trash rack with respect to the horizontal in °, m = discharge coefficient for the trash rack, b = width of the Tyrolean intake in m, L = length of the trash rack in m.
The various coefficients can be taken from Fig. 40.

Fig. 40: Design of a bottom intake (Tyrolean weir)

b	c	b	c
0°	1.000	14°	0.879
2°	0.980	16°	0.865
4°	0.961	18°	0.851
6°	0.944	20°	0.837
8°	0.927	22°	0.825
10°	0.910	24°	0.812
12°	0.894	26°	0.800

values k
The oblique arrangement of the trash rack prevents it from being clogged by bed load or floating matter and the intake from being obstructed. The Tyrolean intake is particularly suitable as an intake structure in rivers transporting bed load. In order to guarantee the diversion of the minimum amount of water when stones become wedged in the trash rack, or branches and leaves remain on the trash rack at low water levels, the trash rack should be

selected L = 1.2 · L_calculated

The collection canal should be designed according to the following principles:

- The canal width should correspond approximately to the length L of the trash rack.
Exactly: B = L cos b, b = angle of inclination of the trash rack bars with respect to the horizontal.
- The canal depth for the evacuation of the water should approximately correspond to the canal width: t ~ B.
- The canal depth is to be so determined that a freeboard of approx. 0.25 · t (t = water depth necessary for the evacuation of the water!) remains up to the upper edge of the trash rack. If the water cannot be evacuated in accordance with the above recommendations, either the gradient or the water depth t of the collection canal must be increased.
- The amount of water for power generation is limited by the capacity of the canal cross-section.