Electrical Machines - Basic vocational knowledge (Institut für Berufliche Entwicklung, 144 p.) 5. Asynchronous motors 5.1. Constructional assembly 5.2. Operating principles 5.2.1. Torque generation 5.2.2. Asynchronous principle 5.2.3. Slip 5.3. Operational behaviour 5.3.1. Start 5.3.2. Rating 5.3.3. Speed control 5.3.4. Rotational sense alteration 5.4. Circuit engineering 5.4.1. Starting connections 5.4.2. Dahlander pole-changing circuit (speed control) 5.4.3. Rotational reversing circuit 5.4.4. Braking circuits 5.5. Application 5.6. Characteristic values of squirrel cage motors

Electrical Machines - Basic vocational knowledge (Institut für Berufliche Entwicklung, 144 p.)

5. Asynchronous motors

5.1. Constructional assembly

The magnetic flow change required in the rotor winding is generated by the stator by means of a circulating field (rotating field).

In this manner the stator aligns itself to a marked extent to the synchronous machine and, like this machine, also features a three phase winding (Cp. Figure 37) able to generate a rotating field. Machines with an operating voltage of 660 V have all winding origins and ends connected to the terminal board. Consequently, the strands can be interlinked in a star-delta arrangement (Cp. Figure 48). In the case of higher operating voltages interlinkage often ensues inside the machine.

Figure 48 - Circuits of the strand windings at the terminal board

U; V; W winding designations

The asynchronous machine is the sole rotating electric machine in which the transmission of electric energy to the rotor does not ensue electromechanically but inductively. Both stator and rotor of the asynchronous machine may be compared to the parts of a transformer whose secondary section has been arranged to rotate.

Two different rotor types of asynchronous motors are customary.

Short-circuit rotor

This rotor has a squirrel cage armature and rods of copper, bronze or aluminium have been positioned in the grooves of the cylindrical rotor lamella pack and short-circuited to each other through end windings.

Figure 49 - Squirrel cage rotor

1 (aluminium, bronze, copper)

Slip ring rotor

The slip ring rotor has a three-phase winding similar to the one of the stator winding.

Figure 50 - Slip-ring rotor

The three spatially positioned coils within 120 degrees are star connected and the origins connected to three slip rings. In operation these slip rings are short-circuited. Thereby there is no difference in the mode of operation of the slip ring rotor and the squirrel cage rotor. Figure 51 shows a sectional presentation of the overall construction of a squirrel cage motor.

Figure 51 - Squirrel cage motor, protection degree IP34 and design IM 1001

1 Stator, 2 Rotor, 3 End shield to the A-side, 4 End shield of the B-side, 5 Ventilator, 6 Ventilator hood, 7 Foot, 8 Bearing lid (external), 9 Bearing lid (internal), 10 Slip-ring capsule, 11 Counterbalance disk, 12 Slip-ring body, 13 Brush holder, 14 Cover sheet, 15...17 Stator terminal boxes

5.2. Operating principles

5.2.1. Torque generation

The rotating field immediately runs at low inertia when a three-phase alternating voltage in connected to the stator winding. During switching on the stator - because of its inertia mass - is still at a standstill. The magnetic flow change resulting from the rotating field induces the voltage U₂ in the rotor. This drives the rotor current I₂ in the short circuited rotor circuit.

Figure 52 - Duplicate of a rotor circuit

U voltage, I current, X_L reactance, R ohmic resistance, Z impeder resistance

The rotor current I₂ is made up of an ohmic share I_2W and a reactive share I_2b

Figure 53 - Indicator diagram of rotor currents

I_b reactive current, I_W eddy current, I₂ rotor current

The ohmic share I_2W of the rotor current makes up the torque along with the rotating field according to the equation

M = c · F₁ · I_2W, and with

I_2W = I₂ · cos j₂

the torque being:

M = C · F₁ · I₂ · cos j₂

The mode of operation of the asynchronous motor can be illustrated by means of the following operating chain

U_I ® I₁ ® F₁ rotating field ® U₂ ® I₂ (I)_2W ® M

5.2.2. Asynchronous principle

Due to the torque effect the rotor begins to rotate in the direction of the rotating field. Commensurately the rotor virtually accepts torque n_D of the rotating field which it, however, never actually attains.

The magnetic flow change dwindles to the extent that the rotor speed draws closer to the speed of the rotating field. Should the rotor attain the speed of the rotating field, then the magnetic flow change is zero. In that case no rotor voltage is induced. Thus, the motor cannot generate a torque.

U₂ = 0 ® I_2W = 0 ® M = 0

The operating condition of the synchronous run cannot be assessed because of the unavoidable idling torque to overcome the friction bearing and air friction, so that the motor must always run in an asynchronous manner.

5.2.3. Slip

Relationship between slip and rotor speed

Rotor speed n lags behind the synchronous speed n_D and one refers to rotor “slippage”. The relative difference n between both speeds, which expresses the relative movement between the stator rotating field and the rotor, is characterised as slip speed n_s in asynchronous machines.

slip speed

n_s = n_rel = n_D - n

The quotient resulting from the slip speed and the rotating field speed has been defined as the slip s

slip

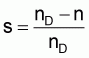
Example:

An asynchronous motor has been connected to a mains voltage of f₁ = 50 Hz frequency. How great is the slip s given a rated speed n = 960 rpm?

Solution:

The rotor rated speed of n = 960 rpm at f₁ = 50 Hz should be aligned to the next synchronous speed n = 1000 rpm.

Thus, the slip can be calculated

The slip accepts at rated load of motors values ranging between one and eight per cent. Greater slip values usually arise in less powerful motors. If we incorporate the speed limit values of the asynchronous machine in motor operation into the equation, we derive the following values for the slip s:

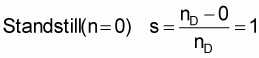
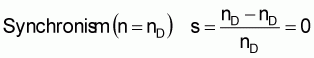
A solution according to the rotor speed yields the following:

sn_D = n_D - n

n = n_D - sn_D

n = n_D (l - s)

Rotor voltage and rotor frequency

Value and frequency of rotor voltage in idling rotors.

The voltage generated by idling rotors is characterized as rotor idling voltage U_2.0

U_2.0 = C₁ · F · n_D

f_2.0 = p · n_D = f₁

The values of the voltage U induced in the rotor and its frequency f₂ depend on the relative speed n_s between the stator rotating field and the rotor, that is to say, the slip. These values are there called slip voltage resp. slip frequency.

Value and frequency of the rotor voltage given any slip speed n_s

U₂ = C₁ · F · n_s

t₂ = p · n_s

If one establishes the quotient U₂/U_2.0 - resp. f₂/f₁, one derives

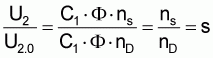
and thus

U₂ = s U_2.0

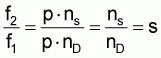
resp. with

w = 2 · p · f

w₂ = s · w₁

The voltage (U₂) induced in the rotor and its frequency f₂ are proportional to the slip.

5.3. Operational behaviour

5.3.1. Start

Inrush current origin

As soon as the current is switched on the rotating field rotates at full speed along the rotor bars of the squirrel cage rotor.

The equation

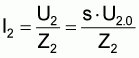
(Cp. Figure 52) indicates that as s = 1 (U = U), a greater inrush current is attained in the rotor which is transmitted transformerwise to the stator side.

Every asynchronous motor accepts a higher current when starting from no-load position.

This inrush current, when utilising the full mains voltage, can be four to eight times as great as the rated current.

This excessive current load can lead to a disruptive voltage drop in the network. Consequently, for example, only motors with a rated performance of up to 2.2 kW may be connected directly to the 380 V network where the making current exceeds the rated current by more than seven times over. Higher powered motors require special measures for cutting back the considerable starting current.

Starting torque

Incorporating the equation

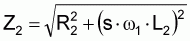
we derive for the rotor current I₂

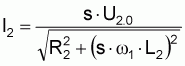
The rotor note only features the small ohmic resistor R₂ but also the inductive resistor

X_L2 = s · w₁ ·L₂ = s · 2 · p · f₁ · L₂

During the switching torque the resistance attains its maximum value as s = 1 and is therefore greater than the ohmic resistance.

Figure 54 - Indicator diagrams of the rotor circuit resistors

Legend as for Figure 52

The power factor cos j₂ therefore attains a minimal value and there is similarly only a low starting torque

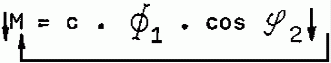
Despite the considerable inrush current the asynchronous motor only evidences a minimal torque when starting from no-load position.

Measures to restrict the starting current

All drive operations presuppose a sound starting up, that is to say, a sufficiently high motor torque. Consequently measures must be undertaken to boost the starting torque. However, the network load which arises during start operations which may be evidenced in a voltage decline or through the inrush current, shall not exceed the prescribed values. It is therefore essential effectively to limit starting current. A simultaneous increase in starting torque is also often requested.

Starting current restriction becomes possible by

- decreasing U_2.0: a lesser stator voltage is fed to the motor (U₁ ~ U_2.0) during starting operations. This leads to a starting procedure for which additional devices are required to connect the short circuit motor.

- increasing R₂: increasing the rotor resistance R whilst starting requires a differently constructed rotor. The short-circuit rotor must be replaced by a differently arranged rotor featuring changeable ohmic resistance facilities.

In the equation M = C₂ · F · I₂ · cos j₂ all physical values have been incorporated which might influence the torque. Such an optimal solution denotes that such values are changed which permit the starting torque to increase without increasing the starting current. This demand is only met if cos j₂ is increased. The power factor is boosted by means of an ohmic resistor at the rotor circuit resistance. This in turn makes necessary a different rotor construction from the short-circuit rotor.

Additional facilities make it possible to decrease the high starting current of the squirrel cage rotor motor (Cp. 5.4.1). A reduction of the starting current whilst simultaneously increasing the starting torque is only possible where differently constructed rotors are used which evidence a greater ohmic resistance during starting operations.

5.3.2. Rating

Speed behaviour depending on the torque

Operating an asynchronous motor presupposes a certain speed for a given torque. This ratio is given for any one motor.

Figure 55 - Rotational behaviour of an asynchronous motor in dependence on the torque

1 Speed, 2 Torque, 3 Rated speed n_n, 4 Starting torque M_a, 5 Rated torque M_n, 6 Breakdown torque M_k

The initial torque M_a is the torque yielded by the motor in no-load operation. The breakdown torque M_k, is the greatest possible motor torque. If this torque is exceeded, the motor comes to a standstill.

The torque at rated load M_n is the motor torque yielded during rated load and rated speed.

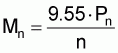
M_n = torque at rated load
P_n = rated power in kW
n = rated speed in rpm.

Every asynchronous motor must be able to accept at least a 160 per cent rated torque for short load spells without motor breakdowns, that is to say the rotor stops. The speed does not vary greatly given considerable load variations.

Operating characteristics of an asynchronous motor

The various motor data about the yielded torque are cited in order to provide an overview of the behaviour of the asynchronous motor between no-load and rated load operation.

This figure indicates the operational curves of an asynchronous motor by means of the following data:

P_n = 4 kW, U = 380 V, I_n = 8.8A, n = 1.430 rpm.

cos j_n = 0.83

Figure 56 - Operating curves of a 4 kW squirrel cage motor (380 V; 8.8 A; cos j = 0.83)

1 Current in amperes
2 Power in kilowatts
3 Power curve
4 Current curve
5 Nominal power

Where asynchronous motors are driven at subload, efficiency and the power factor assume lesser values.

Therefore, asynchronous motors should not be overdimensioned or run in no-load operation.

5.3.3. Speed control

Many drives, for example in the textile or wood-working industries, require speeds considerably greater than 3000 rpm.

Conversely, sometimes low speeds are similarly necessitated. Thus, speed control of the asynchronous motor becomes essential. Speed control possibilities for asynchronous motors can be derived from the following equation:

n = n_D (l - s)

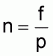
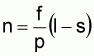
The speed established given a certain torque can therefore be influenced by:

- frequency change in the supplied three-phase alternating current through the employment of rotating frequency converters of through alternating or converter circuits with adjustable frequencies.

- altering the number of pole pairs through pole changing. This can ensue in two ways. Either by means of two or several separate stator windings which can be switched on as desired or by switching over parts of a single stator winding (Dahlander pole-changing circuit).

- altering the slip by changing the voltage application U_I by means of series resistors or adjustable transformers, resp. by changing the ohmic resistance R₂ in the rotor circuit (slip ring rotor).

The most commonly employed adjustment procedures are those of circuit engineering as cited in section 5.4.2.

5.3.4. Rotational sense alteration

Any change in the rotational sense in the case of an asynchronous motor can be attained by changing the rotational direction of the rotating field by exchanging any two external conductors in accordance with Figure 57.

Figure 57 - Rotational sense change

L... conductor U; V; W winding connections (terminal board)

5.4. Circuit engineering

5.4.1. Starting connections

Star-Delta connection

Mode of operation

The star-delta connection is mainly used for low and medium powered machines. During starting the stator winding is star-switched and subsequently delta-switched during acceleration.

In order to be switchable from star to delta the stator windings must be laid out for interlinked (conductor) voltage.

Figure 58 - Voltages and currents during delta starting

1 Conductor voltage
2 Conductor current
3 Strand voltage (voltage through a winding)
4 Strand current (current in a winding)

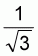
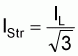
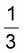
Figure 58 shows that a star connection to a winding strand only receives of the network voltage. The current decreases by the same factor. Moreover as both conductor and strand current in the star connection remain identical (in the delta connection ), a further current reduction by the factor ensues vis-à-vis the star delta connection.

lIStr = IL
	UStr = UL

The considerable starting current is effectively restricted by switching the stator winding from the operational delta connection to the star connection. The conductor current of the star connection is one third of the value of the delta connection.

Moreover, the diminished voltage in the star connection not only causes a diminished stator current; the following also applies;

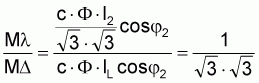
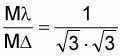
The initial torque in the star connection is but one third of its value in the delta connection.

The advantage of the star-delta connection for limiting the considerable starting current in an effective manner is, however, only possible through a further reduction in the already minimal initial torque. In many cases it will be necessary when employing this starting procedure to start up the motor without load.

Circuitry

Figure 59 - Automatic star-delta connection (main circuit)

L...	external conductor
N...	neutral conductor
F1	Fuses
F2	Thermal cut-out
K1	Main contactor
K2	Delta contactor
K3	Star contactor
M1	Three-phase motor

Figure 60 - Automatic star-delta connection (control circuit)

S1; S2	switches
K1...K3	as in Figure 59
K4	time relay
S; Ö	closers resp. openers of the contactors resp. relay in the commensurate current thread

Circuitry description

Starting up of the squirrel cage motor via K1 and K3 in star connection. Switching the stator winding to delta connection by means of K2. Actuating S2 switched K3 and the timing relay K4 (starting delay). K1 is switched by means of K3 closer. K1 holds itself alone above its closer. Following the adjustment period the opening contact of K4 switches K3 off whilst K2 is switched on by means of the opening contact of K3.

Stator starting resistors

Mode of operation

A further possibility of diminishing stator voltage, thereby reducing motor current whilst starting, is to connect resistors in series to the stator windings (Figure 61). Ohmic resistors are advantageous for lesser powered motors whilst series reactors are more economical for higher powered motors.

Curtailing voltage at the stator windings serves to reduce starting current and starting torque as also applies in other starting procedures.

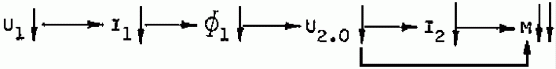
An effective reduction in starting current is attained by connecting resistors in series within the stator circuit in conjunction with a pronounced decline in starting torque.

This procedure is however only suitable for no-load running motors. In order to ensure a smoother and slower starting (i.e. to exclude torque impulses from impact-switched gears) it is sufficient whilst starting to connect an ohmic resistance or a coil in a lead (Kusa circuit). The significance of this resistance is illustrated in the following for both limit values.

Rv ® ¥	The limit current motor is fed from one side only from the stator. Consequently there is no rotating field and the motor does not develop a torque.
Rv = 0	The asynchronous motor is connected directly. The motor develops the maximum possible torque.

With the help of the resistor Rv in a lead it becomes possible to adjust the possible starting torques between zero and the possible maximum value. Impact-free starting becomes possible. As a result of the circuit asymmetry the conduction currents are distributed unequally in the three leads. An effective reduction of starting current is not possible. Current only declines in the strand with the series connected resistor.

Circuitry

Figure 61 - Starting connection by means of series resistors (main circuit)

K2	Starting contactor
R1	Starting resistance

Figure 62 - Starting connection by means of series resistors (control circuit)

K3 Time relay

Circuitry description

Starting ensues via protection K2 and the series resistor R1. Diminish voltage at the stator winding, curtail starting current to ensure smooth starting up. Switching over to network voltage by means of protection K1 without currentless interruption.

Actuating S2 switches on protection K2 and the time relay K2 (initial torque delay). K2 retains itself independently over its closer in the current path two. Following the adjustment spell the K3 closer in the current path switches K1 on whilst K1 switches K2 through its oponer in current path one.

Circuitry of the Kusa circuit

Figure 63 - Kusa circuit 1 (main circuit)

Figure 64 - Kusa circuit 1 (control circuit)

Figure 65 - Kusa circuit 2 (main circuit)

Figure 66 - Kusa circuit 2 (control circuit)

Description of the Kusa circuit

Circuit 1.

By actuating S2 K1 and the time relay K3 are switched on (initial torque delay). K1 is retained independently above its closer in current path 2. Following the adjustment spell the closer of K3 in current path 3 switches on K2 which maintains itself above its closer in current path 4 and switches K3 off by means of its opener in current path 2.

Circuit 2.

By actuating S2 K1 and the time relay K2 (initial torque delay) are switched on. Following the adjustment spell R1 is short-circuited by the closer of the time relay (in Figure 65).

Slip ring motor

Mode of operation

The ends of the rotor winding are attached to the slip rings which gave rise to the designation of this rotor (fig. 67).

The torque and rotor current can be aligned in the desired values during the starting operation with the assistance of the additional resistors which may be switched on via the slip rings of the rotor winding. The internal electrical properties of this motor can be undertaken by switching on the resistors from outside. Starting can thus ensue with substantially less current than in the case of squirrel cage motors whilst the initial torque attains substantial values because of the greater ohmic share in rotor current.

Figure 67 - Slip-ring rotor with rotor starting resistance

1 Rotor starting resistance
K; L; M Connecting terminals

Slip ring motors develop a pronounced initial torque notwithstanding minimal current take-up. They can start up under load.

Slip ring motors are suitable for long and repetitive operating spells.

Switching on rotor starting resistors ensures that current heat losses through greater resistance generally arise outside the motor and, consequently, the motor is not excessively heated up. The starting resistors dissipate heat quickly.

By and large the starter comprises a fixed resistor with several resistance steps which are progressively switched off during the starting operation.

Circuitry

Figure 68 - Automatic starting connection for the slip-ring motor (main circuit)

Figure 69 - Automatic starting connection for the slip-ring motor (control current)

Circuitry description

Figure 68/69 features an automatic starting circuit for ring motors. The starting resistors are switched off by protectors with turn-on delayed closers in three stages.

5.4.2. Dahlander pole-changing circuit (speed control)

Mode of operation

Where several separate electrical windings with varying numbers of pole pairs are required for the stator of the asynchronous motor or windings whose pole pair numbers can be varied by switching over the windings then the speed of the rotating field changes and, thus, also the rotor speed. Squirrel cage motors are used for this purpose because, as opposed to slip ring rotor motors, they are not bound by a specific pole pair. The pole-changing winding in the so-called Dahlander pole-changing circuit is thereby the most perceptible practical feature. This pole-changing winding permits a speed change in the ratio two to one. These circuits have been set out in fig. 70.

The coil groups are switched over from series to parallel connection where a smaller pole pair number is selected, that is to say a greater speed is selected.

Figure 70 - Dahlander connection

(1) Delta connection for low speed (p = 2)
(2) Double star connection for higher speed (p = 1)
...U; ...V; ...W Partial windings

The speeds of asynchronous motors can be roughly stipulated by altering the pole pair number.

Where a stator has been executed with two separate windings which are both pole-reversible, then the speed may be established in four stages, for example, by means of the synchronous speeds of 500 - 750 - 1000 and 1500 rpm.

Motors with changeable pole pair numbers are frequently used for controlling machine tools where approximate setting is usually sufficient. Such motors are also used to drive pumps, ventilators, escalators etc.

Circuitry

Figure 71 - Dahlander connection (main circuit)

Figure 72 - Dahlander circuit (control circuit)

Circuitry description

The protection K1 that the series-switched coil halves of each stand of the stator winding are delta-connected.

The pole pair number p¹ conditions the rotating field speed n¹. The protections K2 and K3 ensure that the coil halves of each strand are parallel connected and the entire stator winding is star connected.

The new pole pair number p² conditions the rotating field speed n². Actuating S3 switches on K1 which retains itself by means of its closer in current path two. K3 and K2 are locked by the openers S3 in the current path five whilst K1 is locked in the current path three. Actuating S2 switches on K2 whose closer switches on K3 in current path five. K1 is locked by opener S2 whilst K3 and K2 are locked in current path one.

5.4.3. Rotational reversing circuit

Mode of operation

Cp. section 5.3.4.

Circuitry

Figure 73 - Rotational direction turnover voltage (main circuit)

Figure 74 - Rotational direction turnover voltage (control circuit)

Circuitry description

Rotational direction selection without cut-off compulsion. The K1 is switched clockwise by actuating S3. K2 is locked in current path three by the openers of K1 and S3. K2 drive is switched counterclockwise by dead and simultaneous actuation of S2 and K1.

5.4.4. Braking circuits

Counter-current braking

Mode of operation

Braking by means of counter-current is the simplest way to attain standstill of an asynchronous drive resp. the deceleration of pull-through loads, for instance in pumping stations. Two stator leads are interchanged to this end during motor operation. This changes the rotational direction of the rotating field. The rotor, which is braked, thus runs counter to the rotational direction of the rotating field. This connection can be used both for squirrel cage and slip ring motors. No additional devices are required.

The braking effect during counter-current braking bases on the altered rotational field direction. The motor tries to accelerate in the other rotational direction.

The motor must be disconnected in good time from the mains so that it does not again accelerate in the new rotational field direction. This is mainly made automatically.

Counter-current operation induces pronounced braking reaction. The current impulse on switching over is considerable greater than starting through direct connection. The motor is generally braked in star connection in order to avoid too great a current.

Figure 75 - Counter-current braking (main circuit)

Figure 76 - Counter-current braking (control circuit)

Circuitry description

Protection K1 switches on the three-phase motor. During switching off K2 connects the mains via two series resistors with two interchanged external conductors. The counter field brakes the rotors.

K2 falls off during motor stillstand.

Actuating S2 switches protection K1 which holds itself in the current path 2 through a closer. K2 is locked by the K1 opener in current path 5 whilst the closer in current path 3 switches the locking relay K3. Switching off by means of S1 the K1 opener closes current path 5. K2 is excited. Given standstill (n = 0) the closer of the automatic brake controller interrupts the F3 current path 5. K3 and K2 drop out.

Direct current braking

Mode of operation

During this braking procedure the machine is disconnected from the mains and the stator winding is excited through direct current. Connection to the direct current source ensues acc. to the circuit depicted in Figure 77.

The stator establishes a constant magnetic field. Induction currents are yielded in the rotor winding which is either short-circuited or connected by means of rotor resistors. These induction currents give rise to a braking torque which facilitates impulse-free braking.

The asynchronous machine with direct current braking behaves in the same manner as an external pole synchronous generator.

Direct current braking is suitable for stopping all categories of asynchronous machine drives. The dissipated heat converted through rotor circuit braking is much less than during counter-braking. The minimal exciting power and the admirably controlled speed of slip ring motors are further advantages of this circuitry.

Figure 77 - Direct current braking (main circuit)

Figure 78 - Direct current braking (control circuit)

Circuitry description

K1 switches on the three-phase motor. On switching off K2 connects direct voltage to the stator winding. K2 drops out after commensurate braking.

Actuating S2 switches protection K1 which holds itself via a closer in current path 2. The K1 closer in current path 3 switches on the auxiliary contactor K3 (release delay). K1 openers in current path 5 serve to lock K2. K1 drops out when S1 switches off. Its opener locks current path 5 (braking ensues through K2) whilst its closer in current path 3 switches K3 off with delay.

The closer of K3 in the current path 5 opens with delay whereby K2 drops off.

5.5. Application

The assembly of an asynchronous motor is much simpler, and therefor also less costly and easier to service, than other motors. This applies in particular to squirrel cage motors. Asynchronous motors are manufactured up to 1000 KW performance. Survey 15 features the characteristic values for asynchronous motors ranging from 0 12 to 4 KW. As speed control still poses some difficulties, asynchronous motors are utilised in the first instance for drives requiring a constant speed. These include, amongst others, compressors, pumps, ventilators, many machine tools and textile machines. Asynchronous motors with attached gears, so-called geared motors, are available for low-speed drives.

The slip ring motor finds application given complicated starting conditions. Slip ring execution makes possible a certain degree of speed control through the additional motor resistor or by means of an additional voltage in the rotor circuit. A slip ring motor also permits counter current braking and, consequently also employment as hoisting gear drives.

5.6. Characteristic values of squirrel cage motors

Survey 15 - Characteristic values of squirrel cage motors between 0.12 and 4 kW (380 V)

Speed	Pn	nn	h	cos jn	In	IA/In	MA/Mn	MK/Mn
rpm	kW	rpm	-	-	A	-	-	-
3000	0.18	2760	0.64	0.81	0.53	4.0	2.1	3.2
	0.25	2780	0.64	0.82	0.77	4.0	2.1	2.4
	0.37	2750	0.68	0.86	0.95	4.3	2.0	2.2
	0.55	2770	0.72	0.86	1.35	4.7	2.1	2.3
	0.75	2800	0.75	0.87	1.75	5.5	2.4	2.7
	1.10	2800	0.77	0.87	2.5	6.1	2.5	2.8
	1.50	2840	0.78	0.85	3.4	6.4	2.5	2.6
	2.20	2820	0.78	0.89	4.7	6.6	2.6	2.7
	3.00	2850	0.82	0.89	6.25	6.7	2.2	2.5
	4.00	2880	0.83	0.87	8.45	6.5	2.2	2.6
1500	0.12	1360	0.56	0.72	0.45	3.0	2.0	2.1
	0.18	1360	0.59	0.73	0.63	3.2	2.2	2.4
	0.25	1370	0.62	0.74	0.82	3.4	1.9	2.1
	0.37	1360	0.67	0.77	1.10	3.6	1.9	2.0
	0.55	1380	0.70	0.77	1.55	4.4	2.0	2.3
	0.75	1380	0.72	0.78	2.0	4.6	2.1	2.3
	1.10	1410	0.77	0.78	2.8	5.6	2.5	2.8
	1.50	1415	0.78	0.76	3.8	6.0	2.4	3.0
	2.20	1425	0.79	0.77	5.55	6.0	2.4	2.9
	3.00	1430	0.81	0.83	6.8	5.8	2.1	2.5
	4.00	1430	0.83	0.83	8.85	6.4	2.5	2.9
1000	0.12	870	0.50	0.61	0.6	2.5	2.1	2.2
	0.18	900	0.56	0.62	0.79	2.7	2.0	2.0
	0.25	900	0.59	0.58	1.1	2.9	2.3	2.4
	0.37	920	0.63	0.7	1.27	3.7	2.3	2.5
	0.55	920	0.67	0.69	1.8	4.0	2.6	2.8
	0.75	930	0.70	0.71	2.3	4.4	2.3	2.4
	1.10	930	0.73	0.73	3.1	4.5	2.2	2.4
	1.50	945	0.77	0.78	3.8	5.1	2.1	2.4
	2.20	945	0.78	0.81	5.3	4.9	2.0	2.4
750	0.12	670	0.44	0.56	0.74	2.2	2.1	2.2
	0.18	690	0.52	0.64	0.82	2.7	2.0	2.4
	0.25	690	0.56	0.63	1.1	3.0	2.3	2.5
	0.37	690	0.60	0.64	1.5	3.2	2.0	2.2
	0.55	690	0.64	0.65	2.0	3.3	2.0	2.1
	0.75	700	0.68	0.68	2.5	3.8	1.9	2.3
	1.10	700	0.70	0.70	3.4	4.0	2.1	2.5
	1.50	700	0.73	0.73	4.3	4.2	2.0	2.4

Questions for repetition and control

1. Explain the assembly of an asynchronous motor and its two different rotor types.

2. How is the torque of a three-phase asynchronous motor attained?

3. What are the effects of increasing shaft load on the speed and current acceptance of the asynchronous motor?

4. When is a three-phase slip ring motor used?

5. Describe the most common starting varieties of a three-phase motor setting out their advantages and disadvantages!

6. The following nominal data have been given for a three-phase motor: 5.5 kW; 1440 rpm; cos j = 0.82; h = 0.8; 380 V. Calculate motor current acceptance level!

7. How can the rotational direction of a three-phase motor be changed?