Digital Teaching Aid (DED Philippinen, 86 p.) Introduction Boolean Algebra - Lesson 2 Lesson Plan Introduction Boolean algebra Boolean equations of logic circuits NOR and NAN gates De Morgan's theorems Worksheet No. 2

Digital Teaching Aid (DED Philippinen, 86 p.)

Introduction Boolean Algebra - Lesson 2

Lesson Plan

Introduction

Titel: Introduction Boolean Algebra

Objectives:

- Able to express the basic operations in Boolean algebra
- Know how to describe a logic circuit in a Boolean equation
- Understand the basic Boolean theorems.

Time	Method		Topic		Way	Remark
	Q/A		* Review Lesson 1		B
	S		* Introduction - George Boole		B
	S		* Boolean algebra		B,Ex
		S,E		- NOT operation
				- OR operation
				- AND operation
		S,E		- Boolean equations of logic circuits	B,Ex
				- NOR gates Truth table	B
		S,D		- De Morgan's 1. theorem	B
				- NAND gates Truth table	B
		E		- De Morgan's 2. theorem	B,HO
	E		* Review Exercise		WS	Worksheet No. 2
	S: Speech D: Discussion Q/A: Question/Answer E: Exercise				B: Boardscript P: Picture Ex: Example HO: Hands-On WS: Worksheet HT: Hand-Out

Boolean algebra

George Boole (1854) invented a new kind of algebra that could be used to analyse and design digital and computer circuits.

NOT operation

Fig. 2-1: Inverter symbol and Boolean notation

Ex: If A is 0 (low) ® X = NOT 0 = 1

In Boolean algebra the overbar stands for NOT operation.

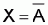
OR operation

Fig. 2-2: OR symbol and Boolean notation

Ex: If A = 0, B = 1 ® X = A or B = 0 or 1 = l

In Boolean algebra the + sign stans for the OR operation:

X = A + B

Ex: If A = 1, B = 0 ® X = A + B = 1 + 0 = 1

AND operation

Fig. 2-3: AND symbol and Boolean notation

In Boolean algebra the multiplication sign stands for the AND operation:

X = A · B

or simply:

X = A B

Ex: If A = 1, B = 0 ® X = A B = 1 · 0 = 0

Boolean equations of logic circuits

You can use Boolean algebra as a shorthand notation for digital circuits.

Ex:

Fig. 2-4: Digital circuit

Output of the first gate:

X3 = A + B

Output of the second gate:

X6 = X3 + C = A + B + C

The final output is:

X8 = X6 + D = A + B + C + D = X

HO: Find the Boolean equation for the following circuit.

Fig. 2-5: Logic circuit

Solution:

X = (A + B) (C + D)

NOR and NAN gates

NOR gate

Based on the three fundamental logic operations it is possible to design additionel logic devices.

Fig. 2-6: NOR gate, symbol and truth table

Formula: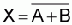

NAND gate

Fig. 2-7: NAND grate, symbol and truth table

Formula: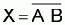

De Morgan's theorems

Augustus De Morgan was the first who found the link between logic and mathematics.

Fig. 2-8: Logic circuits with the same output

Although the circuits are different but the output, as we can see in the truth table, is equal. Therefore we can write:

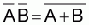
De Morgan's First Theorem

Also if we compare the two circuits on the next page we can easily see that the output is the same, although the circuits are different.

(see Fig. 2-9)

Fig. 2-9: Logic circuits with the same output

So we can write:

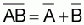
De Morgan's Second Theorem

HO: How can you connect a NAND gate to get an inverter

Solution:

Figure

HO: How can you connect NAND gates to get an OR gate?

Solution:

Figure

Worksheet No. 2

No. 1 What is the Boolean equation? What is the truth table?

No. 2 What is the Boolean equation? What is the truth table?

No. 3 What is the Boolean equation? What is the truth table?

No. 4 Construct the truth table.

No. 5 Draw the logic circuit whose Boolean equation is

Use the 7404 and the 7432 with pin numbers

No. 6 Draw the logic circuit whose Boolean equation is

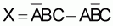
Use the 7404, 7432 and the 7411 with pin numbers.